Sysuke's World

Appearance

遇到一道二叉树的题目时的通用思考过程是：

是否可以通过遍历一遍二叉树得到答案？如果不能的话，是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？

1.二叉树 ​

做二叉树的问题，关键是把题目的要求细化，搞清楚根节点应该做什么，然后剩下的事情抛给前/中/后序的遍历框架就行了。比如对于一般的构造二叉树的题目，是要想怎么构造出根节点。所以应该是前序遍历。

javascript
/* 二叉树遍历框架 */
function traverse(root) {
    if (root == null) return;
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

中序遍历的非递归实现

javascript
// https://leetcode-cn.com/problems/convert-bst-to-greater-tree/solution/shou-hua-tu-jie-zhong-xu-bian-li-fan-xiang-de-by-x/
const inorderTraversal = (root) => {
  const res = [];
  const stack = [];

  while (root) {        // 能压入栈的左子节点都压进来
    stack.push(root);
    root = root.left;
  }
  while (stack.length) {
    let node = stack.pop(); // 栈顶的节点出栈
    res.push(node.val);     // 在压入右子树之前，处理它的数值部分（因为中序遍历）
    node = node.right;      // 获取它的右子树
    while (node) {          // 右子树存在，执行while循环    
      stack.push(node);     // 压入当前root
      node = node.left;     // 不断压入左子节点
    }
  }
  return res;
};

路径总和 ​

递归： 深度优先遍历

javascript
var hasPathSum = function(root, targetSum) {
    if(root === null) return false
    if(root.left === null && root.right === null && root.val === targetSum) return true
    return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val)
};

广度优先遍历: 父节点的值是targetSum - root.val

javascript
var hasPathSum = function(root, targetSum) {
    if(root === null) return false
    let stack = [root]
    root.val = targetSum - root.val
    while(stack.length) {
        const nextNodes = []
        for(let i = 0; i < stack.length; i++) {
            let node = stack[i]
            if(node.left === null && node.right === null && node.val === 0) {
                return true
            }
            if(node.left) {
                node.left.val = node.val - node.left.val
                nextNodes.push(node.left)
            }
            if(node.right) {
                node.right.val = node.val - node.right.val
                nextNodes.push(node.right)
            }
        }
        stack = nextNodes
    }
    return false
};

二叉树的层序遍历 ​

bfs

javascript
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if(root == null) return []
    let queue = [root]
    const res = []
    while(queue.length) {
        const nodesLevels = []
        const newQueue = []
        queue.forEach(node => {
            nodesLevels.push(node.val)
            if (node.left) newQueue.push(node.left)
            if (node.right) newQueue.push(node.right)
        })
        res.push(nodesLevels)
        queue = newQueue
    }
    return res
};

dfs

javascript
var levelOrder = function(root) {
    if(root == null) return []
    const res = []
    const dfs = (node, step) => {
        if(node === null) return
        if(!res[step]) res[step] = []
        res[step].push(node.val)
        dfs(node.left, step + 1)
        dfs(node.right, step + 1)
    }
    dfs(root, 0)
    return res
};

二叉树的序列化与反序列化 ​

前序遍历法，后续遍历法差不多一样，而中序遍历的方式行不通，因为无法实现反序列化方法deserialize。

javascript
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */

const splitStr = ','
const nullStr = '#'

var serialize = function(root) {
    let res = ''
    

    function help(node) {
        if(node === null) {
            res = res  + nullStr + splitStr
            return
        }
        res = res  + node.val + splitStr
        help(node.left)
        help(node.right)
    }

    help(root)

    return res.slice(0, res.length - 1)  // 末尾多一个,
};

/**
 * Decodes your encoded data to tree.
 *
 * @param {string} data
 * @return {TreeNode}
 */
var deserialize = function(data) {
    const nodes = data.split(splitStr)

    function help(nodes) {
        if (nodes.length === 0) return null
        const node = nodes.shift()
        if (node === nullStr) return null
        const root = new TreeNode(parseInt(node))
        root.left = help(nodes)
        root.right = help(nodes)
        return root
    }

    return help(nodes)
};

/**
 * Your functions will be called as such:
 * deserialize(serialize(root));
 */

验证二叉树的前序序列化 ​

javascript
// https://leetcode-cn.com/problems/verify-preorder-serialization-of-a-binary-tree/solution/pai-an-jiao-jue-de-liang-chong-jie-fa-zh-66nt/
/**
 * @param {string} preorder
 * @return {boolean}
 */
var isValidSerialization = function(preorder) {
    const nodes = preorder.split(',')
    const stack = []
    for(let i = 0; i < nodes.length;i++) {
        stack.push(nodes[i])
        while(stack.length > 2 && stack[stack.length - 1] === '#' && stack[stack.length - 2] === '#' && stack[stack.length - 3] !== '#') {
            stack.pop()
            stack.pop()
            stack.pop()
            stack.push('#')
        }
    }
    return stack.length === 1 && stack.pop() === '#'
};

从前序与中序遍历序列构造二叉树 ​

先构造根节点，接着思考如何构造左右节点，而构造左右节点也是构造根节点。剩下的就是分割数组

javascript
var buildTree = function(preorder, inorder) {
    if (preorder.length === 0) return null
    const root = new TreeNode(preorder[0])
    const inorderRootIndex = inorder.findIndex(v => v === preorder[0])
    root.left = buildTree(preorder.slice(1,inorderRootIndex + 1), inorder.slice(0, inorderRootIndex)) 
    root.right = buildTree(preorder.slice(inorderRootIndex+1), inorder.slice(inorderRootIndex+1))
    return root
};

从中序与后序遍历序列构造二叉树 ​

javascript
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(inorder, postorder) {
    if(inorder.length === 0) return null
    const rootValue = postorder[postorder.length -1]
    const root = new TreeNode(rootValue)
    const inorderFindIndex = inorder.findIndex(v => v === rootValue) // 1
    root.left = buildTree(inorder.slice(0, inorderFindIndex), postorder.slice(0, inorderFindIndex))
    root.right = buildTree(inorder.slice(inorderFindIndex+1), postorder.slice(inorderFindIndex, postorder.length -1))
    return root
};

对称二叉树 ​

递归

javascript
var isSymmetric = function(root) {
    function check(left, right) {
        if(left === null && right === null) return true
        else if(left && right) {
            return left.val === right.val && check(left.left, right.right) && check(left.right, right.left)
        } else return false
    }

    if(root === null) return true
    return check(root.left, root.right)
};

迭代

javascript
var isSymmetric = function(root) {
  if (!root) return true;
  let stack = [];
  stack.push(root.left, root.right);
  while (stack.length) {
    const right = stack.pop();
    const left = stack.pop();
    if (left === null && right === null) {
      // 节点为空什么都不做
    } else if (left && right && left.val === right.val) {
      //左左节点和对称右右节点入栈
      stack.push(left.left);
      stack.push(right.right);
      //左右节点和对称右左节点入栈
      stack.push(left.right);
      stack.push(right.left);
    } else {
      return false;
    }
  }
  return true;
};

翻转二叉树 ​

javascript
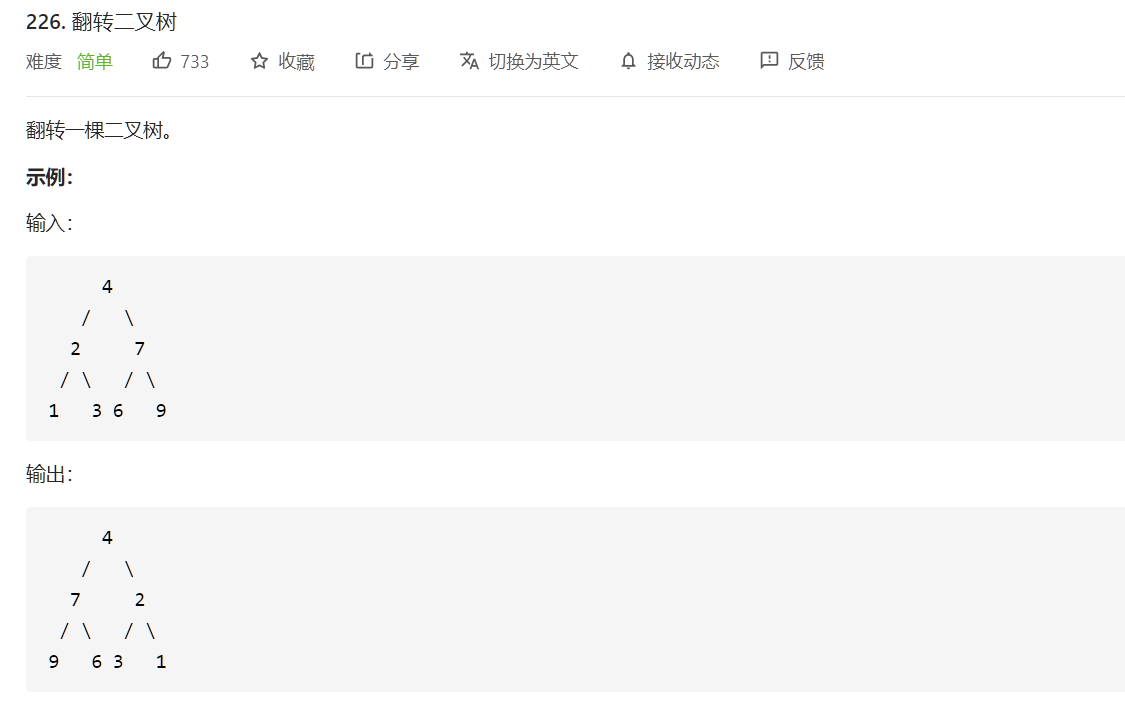
var invertTree = function(root) {
    if (root === null) return null
    let temp = root.left
    root.left = root.right
    root.right = temp
    invertTree(root.right)
    invertTree(root.left)
    return root
};

填充每个节点的下一个右侧节点指针 ​

javascript
var connect = function(root) {
    if(root === null) return null
    connectTowNode(root.left, root.right)
    return root
};

function connectTowNode(left, right) {
    if (left === null || right === null) {
        return
    }
    left.next = right
    connectTowNode(left.left,left.right)
    connectTowNode(right.left,right.right)
    connectTowNode(left.right, right.left)
}

二叉树展开为链表 ​

javascript
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
    if (root === null) return null
    flatten(root.left)
    flatten(root.right)
    let left = root.left, right = root.right
    root.right = left
    root.left = null
    let node = root
    while(node.right !== null) {
        node = node.right
    }
    node.right = right
};

var flatten2 = function(root) {
    while(root){
      let p=root.left;
      if(p){
        while(p.right) p=p.right;
        p.right=root.right;
        root.right=root.left;
        root.left=null
      }
      root=root.right;
    }
    
};
// 链接：https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/solution/114er-cha-shu-zhan-kai-wei-lian-biao-chao-jian-dan/

二叉树的最近公共祖先 ​

javascript
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    if(root === null) return null
    if(root === q || root === p) return root
    const left = lowestCommonAncestor(root.left, p, q)
    const right = lowestCommonAncestor(root.right, p, q)

    if(left && right) return root
    else if (left) return left
    else if(right) return right
    else return null
};
javascript
// https://www.nowcoder.com/practice/e0cc33a83afe4530bcec46eba3325116
/**
 * 
 * @param root TreeNode类 
 * @param o1 int整型 
 * @param o2 int整型 
 * @return int整型
 */
function lowestCommonAncestor( root ,  o1 ,  o2 ) {
    // write code here
    if(root === null) return -1
    if(root.val === o1 || root.val === o2) return root.val
    
    const left = lowestCommonAncestor(root.left, o1,o2)
    const right = lowestCommonAncestor(root.right, o1,o2)
    
     if (left !== -1 && right !== -1) return root.val;
     else if (left != -1) return left;
     else if (right != -1) return right;
     else return -1;
}

二叉树的最大深度 ​

js
// bfs
const maxDepth = (root) => {
  if (root == null) return 0;
  const queue = [root];
  let depth = 1;
  while (queue.length) {
    // 当前层的节点个数
    const levelSize = queue.length;
    // 逐个让当前层的节点出列
    for (let i = 0; i < levelSize; i++) {
      // 当前出列的节点
      const cur = queue.shift();
      // 左右子节点入列
      if (cur.left) queue.push(cur.left);
      if (cur.right) queue.push(cur.right);
    }
    // 当前层所有节点已经出列，如果队列不为空，说明有下一层节点，depth+1
    if (queue.length) depth++;
  }
  return depth;
};

// 动态规划思路 - DFS
var maxDepth = function(root) {
  if (root === null) return 0
  const leftMax = maxDepth(root.left)
  const rightMax = maxDepth(root.right)
  // 根据左右子树的最大深度推出原二叉树的最大深度
  return 1 + Math.max(leftMax, rightMax)
};

最大二叉树 ​

javascript
var constructMaximumBinaryTree = function(nums) {
    if(nums.length === 0) return null
    const [max, leftArray, rightArray] = getBuildResult(nums)
    const root = new TreeNode(max)
    root.left = constructMaximumBinaryTree(leftArray)
    root.right = constructMaximumBinaryTree(rightArray)
    return root
};

function getBuildResult(arr) {
    const max = Math.max(...arr)
    const maxIndex = arr.findIndex(v => v === max)
    return [
        max,
        arr.slice(0, maxIndex),
        arr.slice(maxIndex+1)
    ]
}

寻找重复的子树 ​

1.拼接字符串使二叉树序列化

2.用Map存放每个子树以及出现的次数

3.递归得到所有的子树

javascript
var findDuplicateSubtrees = function(root) {
    const treeMap = new Map()
    const result = []
    function traversal(root) {
        if(!root) {
            return '#'
        }
        const left = traversal(root.left)
        const right = traversal(root.right)
        const subtree = `${left},${right},${root.val}`
        if(treeMap.get(subtree)) {
            treeMap.set(subtree, treeMap.get(subtree)+1)
        } else {
            treeMap.set(subtree, 1)
        }
        if(treeMap.get(subtree) === 2) {
            result.push(root)
        }
        return subtree
    }
    traversal(root)
    return result
};
  1. 二分查找
javascript

二叉树的直径 ​

javascript
var diameterOfBinaryTree = function(root) {
    let maxLength = 0;
    function trverse(root) {
         if (root === null) return 0;
         const leftMax = trverse(root.left);
         const rightMax = trverse(root.right);
         const max = leftMax + rightMax;
         maxLength = Math.max(maxLength, max);
         return Math.max(leftMax, rightMax) + 1;
    }
    trverse(root);
    return maxLength;
};

求二叉树中最大路径和 ​

javascript
var maxPathSum = function(root) {
    let res = -Infinity
    function help(node) {
        if (node === null) return 0
        let left = Math.max(0, help(node.left))
        let right = Math.max(0, help(node.right))
        res = Math.max(res, left + right + node.val)
        return Math.max(left, right) + node.val
    }
    help(root)
    return res
};

求根节点到叶节点数字之和 ​

dfs

javascript
var sumNumbers = function(root) {
    let arr = []
    function help(node, str) {
        if(!node) return
        str = str + node.val
        if(node.left === null && node.right === null) {
            if(str) arr.push(str)
            return
        }
        help(node.left, str)
        help(node.right, str)
    }
    help(root, '')
    return arr.reduce((prev, curr) => parseInt(curr) + parseInt(prev), 0)
};
// 官方的
const dfs = (root, prevSum) => {
    if (root === null) {
        return 0;
    }
    const sum = prevSum * 10 + root.val;
    if (root.left == null && root.right == null) {
        return sum;
    } else {
        return dfs(root.left, sum) + dfs(root.right, sum);
    }
}
var sumNumbers = function(root) {
    return dfs(root, 0);
};

bfs

javascript
var sumNumbers = function(root) {
    if (root === null) {
        return 0;
    }
    let sum = 0;
    const nodeQueue = [];
    const numQueue = [];
    nodeQueue.push(root);
    numQueue.push(root.val);
    while (nodeQueue.length) {
        const node = nodeQueue.shift();
        const num = numQueue.shift();
        const left = node.left, right = node.right;
        if (left === null && right === null) {
            sum += num;
        } else {
            if (left !== null) {
                nodeQueue.push(left);
                numQueue.push(num * 10 + left.val);
            }
            if (right !== null) {
                nodeQueue.push(right);
                numQueue.push(num * 10 + right.val);
            }
        }
    }
    return sum;
};

2.二叉搜索树 ​

BST(Binary Search Tree) 的特性

  1. 对于 BST 的每一个节点node，左子树节点的值都比node的值要小，右子树节点的值都比node的值大。
  2. 对于 BST 的每一个节点node，它的左侧子树和右侧子树都是 BST。

从做算法题的角度来看 BST，除了它的定义，还有一个重要的性质：BST 的中序遍历结果是有序的（升序）。

typescript
interface TreeNode {
  left: null | TreeNode,
  right: null | TreeNode,
  val: number
}
function traverse(root:TreeNode) {
    if (root == null) return;
    traverse(root.left);
    // 中序遍历代码位置
    console.log(root.val);
    traverse(root.right);
}

二叉搜索树中第K小的元素 ​

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

javascript
var kthSmallest = function(root, k) {
  let res = null
  let rank = 0
  function treverse(node) {
    if (node === null) return
    treverse(node.left)
    rank++
    if (rank === k) {
      res = node.val
      return
    }
    treverse(node.right)
  }
  treverse(root)
  return res
}

迭代

javascript
let kthSmallest = function(root, k) {
    let stack = []
    let node = root
    
    while(node || stack.length) {
        // 遍历左子树
        while(node) {
            stack.push(node)
            node = node.left
        }
      
        node = stack.pop()
        if(--k === 0) {
            return node.val
        }
        node = node.right
    }
    return null
}

把二叉搜索树转换为累加树 ​

javascript
var convertBST = function(root) {
    let prevSum = 0
    function help(node) {
        if (node === null) return
        help(node.right)
        node.val = node.val + prevSum
        prevSum = node.val
        help(node.left)
    }
    help(root)
    return root
};

迭代版本

javascript
var convertBST1 = function(root) {
    if (root === null) return null
    let prevSum = 0
    let stack = []
    let curr = root
    while(curr) {
        stack.push(curr)
        curr = curr.right
    }
    while(stack.length) {
        let node = stack.pop()
        node.val = node.val + prevSum
        prevSum = node.val
        node = node.left
        while(node) {
            stack.push(node)
            node = node.right
        }
    }
    return root
};

const convertBST = (root) => {
  let sum = 0;
  let stack = [];
  let cur = root;

  while (cur) {  // 右子节点先不断压栈
    stack.push(cur);
    cur = cur.right;
  }

  while (stack.length) {  // 一直到清空递归栈
    cur = stack.pop();    // 位于栈顶的节点出栈
    sum += cur.val;       // 做事情
    cur.val = sum;        // 做事情
    cur = cur.left;       // 找左子节点
    while (cur) {         // 存在，让左子节点压栈
      stack.push(cur);    // 
      cur = cur.right;    // 让当前左子节点的右子节点不断压栈
    }
  }

  return root;
};

恢复二叉搜索树 ​

javascript
// https://leetcode-cn.com/problems/recover-binary-search-tree/solution/tu-jie-hui-fu-yi-ge-er-cha-sou-suo-shu-by-hyj8/
var recoverTree = function(root) {
    let prev = new TreeNode(-Infinity)
    let err1 = null, err2 = null

    function trverseTree(node) {
        if(node === null) return
        trverseTree(node.left)
        if(err1 === null && prev.val > node.val) {
            err1 = prev
        }  
        if(err1 !== null && prev.val > node.val) {
            err2 = node
        }
        prev = node
        trverseTree(node.right)
    }

    trverseTree(root)
    let temp = err1.val
    err1.val = err2.val
    err2.val = temp
};

判断BST的合法性 ​

javascript
function isValidBST(root) {
  /* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
  function isValidBST(root, min, max) {
    // base case
    if (root === null) return true
    // 若 root.val 不符合 max 和 min 的限制，说明不是合法 BST
    if (min !== null && root.val <= min.val) return false
    if (max !== null && root.val >= max.val) return false
    return isValidBST(root.left, min, root) && isValidBST(root.right, root, max)
  }

  return isValidBST(root, null, null)
}

中序遍历

javascript
var isValidBST = function(root) {
    let stack = [];
    let inorder = -Infinity;

    while (stack.length || root !== null) {
        while (root !== null) {
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();
        // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
        if (root.val <= inorder) {
            return false;
        }
        inorder = root.val;
        root = root.right;
    }
    return true;
};

在BST中搜索一个数 ​

javascript
function isInBST(root, target) {
  if (root === null) return true
  if (root.val === target) return true
  if (root.val > target) return isInBST(root.left, target)
  if (root.val < target) return isInBST(root.right, target)
}

不同的二叉搜索树 ​

动态规划

假设n个节点存在二叉排序树的个数是G(n)，令f(i)为以i为根的二叉搜索树的个数

即有:G(n) = f(1) + f(2) + f(3) + f(4) + ... + f(n)

n为根节点，当i为根节点时，其左子树节点个数为[1,2,3,...,i-1]，右子树节点个数为[i+1,i+2,...n]，所以当i为根节点时，其左子树节点个数为i-1个，右子树节点为n-i，即f(i) = G(i-1)*G(n-i),

上面两式可得:G(n) = G(0)*G(n-1)+G(1)*(n-2)+...+G(n-1)*G(0)

javascript
/**
 * @param {number} n
 * @return {number}
 */
var numTrees = function(n) {
    const dp = new Array(n + 1).fill(0);
    dp[0] = 1;
    dp[1] = 1;

    for (let i = 2; i <= n; ++i) {
        for (let j = 1; j <= i; ++j) {
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }
    return dp[n];
}

In case I don't see you. Good afternoon, good evening, and good night.

Copyright © 2019-present Sysuke