Sysuke's World

Appearance

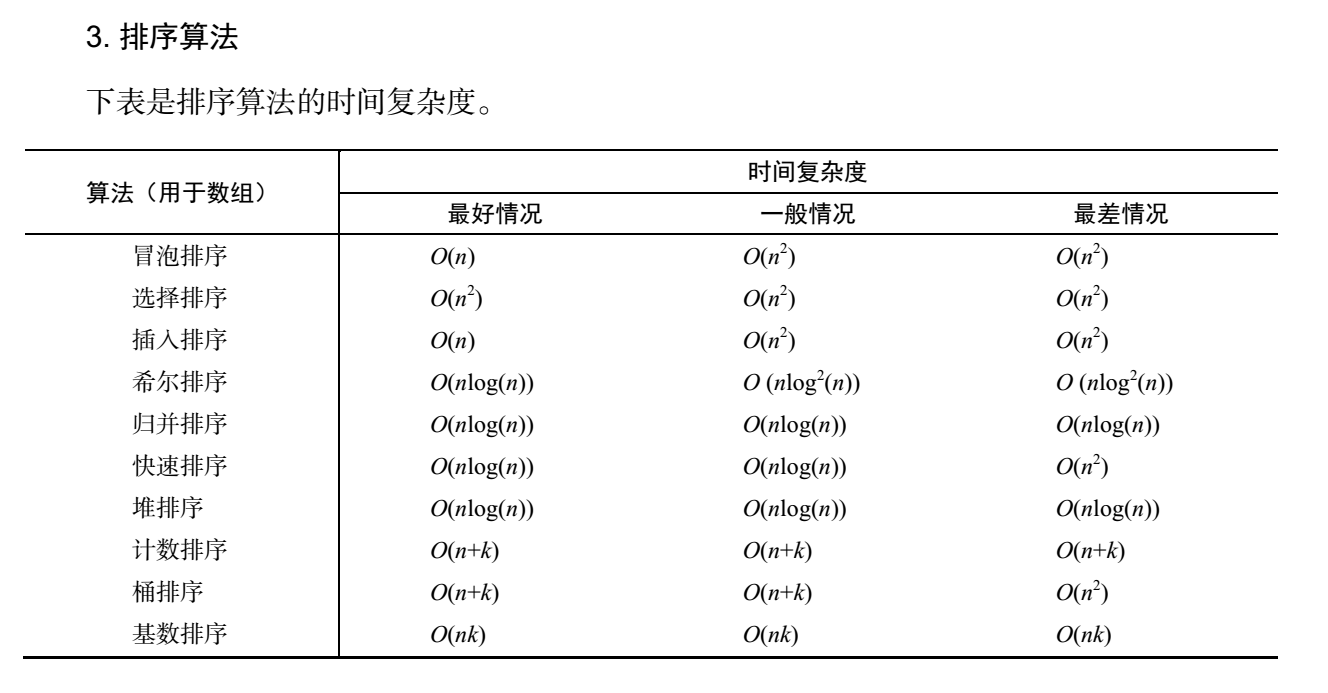
排序算法 ​

An image

动图演示

1. 冒泡排序 ​

冒泡排序比较所有相邻的两个项，如果第一个比第二个大，则交换它们。元素项向上移动至 正确的顺序，就好像气泡升至表面一样。

javascript
function bubbleSort (arr) {

	const len = arr.length

	for (let i = 0; i < len - 1; i++) {
		for (let j = 0; j < len - 1 - i; j++) {
			if (arr[j] > arr[j + 1]) {
				// let temp = arr[j]
				// arr[j] = arr[j + 1]
				// arr[j +1] = temp
				[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
			}
		}
	}

	return arr

}

2. 选择排序 ​

选择排序大致的思路是找到数据结构中的最小值并 将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。

javascript
function selectionSort (arr) {
	const len = arr.length

	for (let i = 0; i < len - 1; i++) {
		let minIndex = i
		for (let j = i + 1; j < len; j++) {
			if (arr[j] < arr[minIndex]) {
				minIndex = j
			}
		}
		if (minIndex !== i) [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
	}

	return arr
}

3. 插入排序 ​

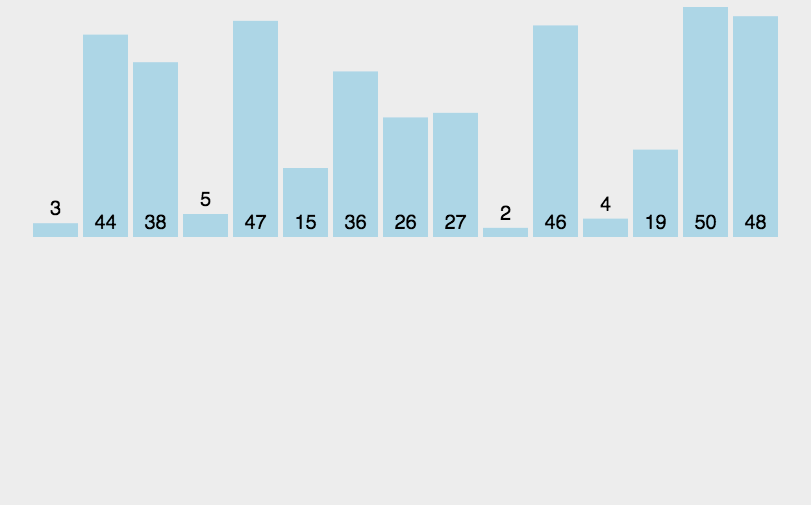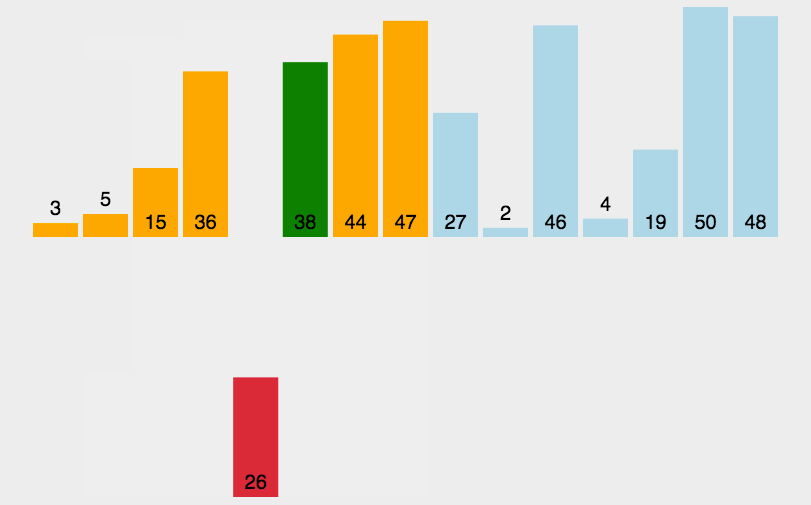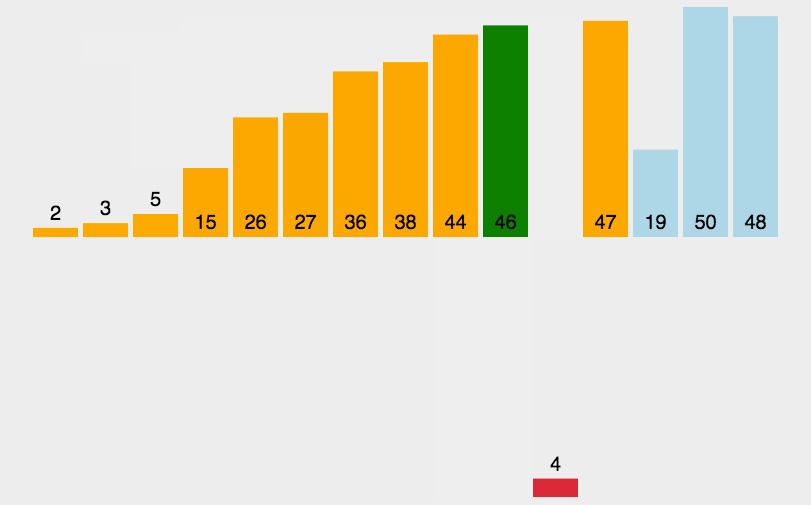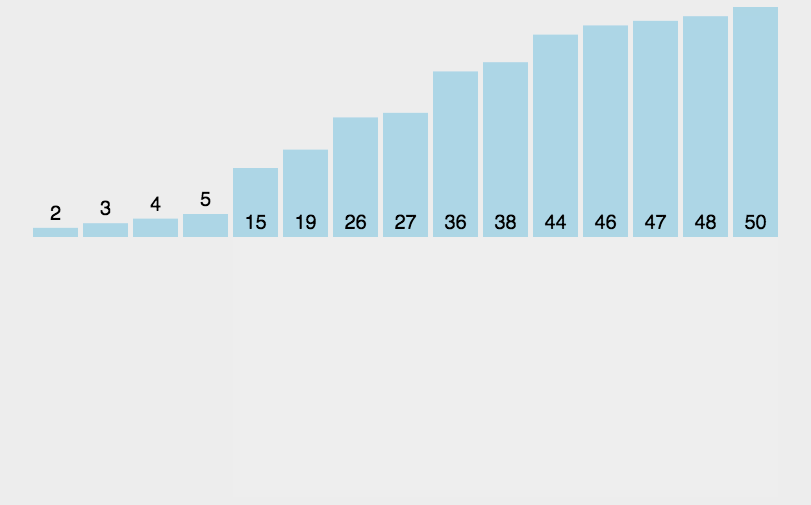
An image

javascript
function insertSort (arr) {

	const len = arr.length

	for (let i = 0; i < len; i++) {
		const v = arr[i + 1]
		let j = i + 1
		while (j > 0) {
			j--
			if (arr[j] > v) {
					[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
			}
		}
	}

	return arr
}

4. 归并排序 ​

An image

Mozilla Firefox 使用归并排序作为 Array.prototype.sort 的实现

原始数组切分成较小的数组，直到每个小数组只 有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。要使用递归。

递归写法

javascript
function mergeSort(arr) {
	if (arr.length > 1) {
		const { length } = arr
		const middle = Math.floor(length / 2)
		const left = mergeSort(arr.slice(0, middle))
		const right = mergeSort(arr.slice(middle))
		arr = merge(left, right)
	}
	return arr
}

function merge(left, right) {
	let i = 0, j = 0
	const result = []
	while (i < left.length && j < right.length) {
		result.push(left[i] < right[j] ? left[i++] : right[j++])
	}
	return result.concat(i < left.length ? left.slice(i) : right.slice(j))
}

// [2, 4, 3, 1]
// left [2, 4]  right [1, 3]
//
// 1  j = 1 i = 0
// 1 2 j = 1 i =1
// 1 2 3 j = 2 i = 1

非递归写法

javascript
function mergePass(arr) { // 将每个元素看作是相邻的数组长度为1。
	let temp = new Array(arr.length), N = arr.length, length = 1
	let t // 迭代深度。
	for (t = 0; Math.pow(2, t) < N; t++, length *= 2) { // 每次跳过的长度翻倍。
		const even = t % 2 === 0 // 复用 arr 和 temp 来回赋值。
		for (let left = 0; left < N; left += 2 * length) { // 左边数组起始位置 left 从0开始。
			const middle = left + length < N ? left + length : left // 右边数组起始位置 middle 就是left + 一个数组长度length 但是不要超过 N 。
			const right = left + (2 * length) < N ? left + (2 * length) : N // 右边界 right 就是 left + 两个数组长度。
			merge2(even ? arr : temp, even ? temp : arr, left, middle, right) // 合并每两个相邻的数组。
		}
	}
	if (t % 2 === 0) {
		return arr//返回arr
	}
	return temp // 返回 temp 。
}

function merge2(arr, temp, left, middle, right) {
	const leftEnd = middle - 1 // 通过右边数组的起始位置得到左边数组的结束位置。
	while (left <= leftEnd && middle < right) { // 如果‘指针’没有越界。
		if (arr[left] > arr[middle]) { // 如果左边数组第一个元素比右边数组第一个元素大。
			temp[left + middle - leftEnd - 1] = arr[middle++] // 将右边数组最小的放入有序数组 temp（初始值为空)。
		} else {
			temp[left + middle - leftEnd - 1] = arr[left++] // 将左边数组最小的放入有序数组 temp（初始值为空)。
		}
	}
	while (left > leftEnd && middle < right) { // 如果左边数组放完了，右边数组还有元素。
		temp[left + middle - leftEnd - 1] = arr[middle++] // 那么依次将右边数组剩余的元素放入 temp 。
	}
	while (left <= leftEnd && middle >= right) { // 如果右边数组放完了，左边数组还有元素
		temp[left + middle - leftEnd - 1] = arr[left++] // 那么依次将左边数组剩余的元素放入 temp 。
	}
}

5. 希尔排序 ​

1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

算法描述 ​

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

  • 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
  • 按增量序列个数k，对序列进行k 趟排序；
  • 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

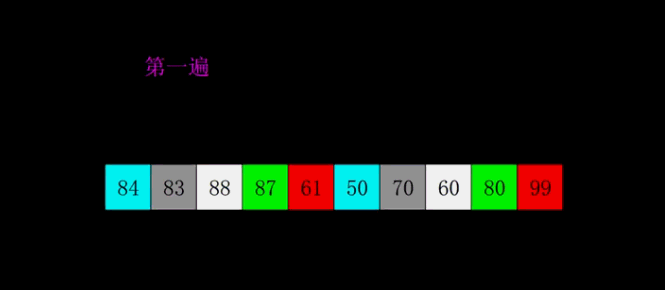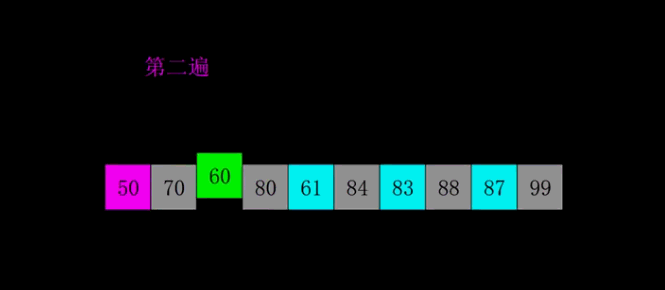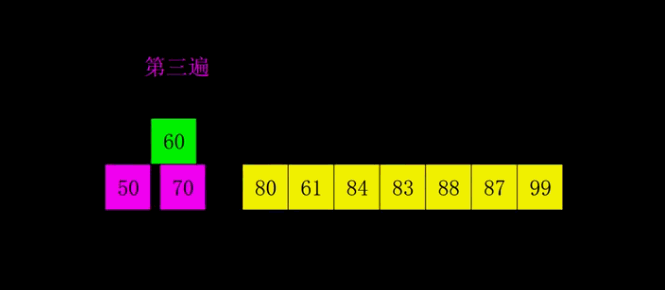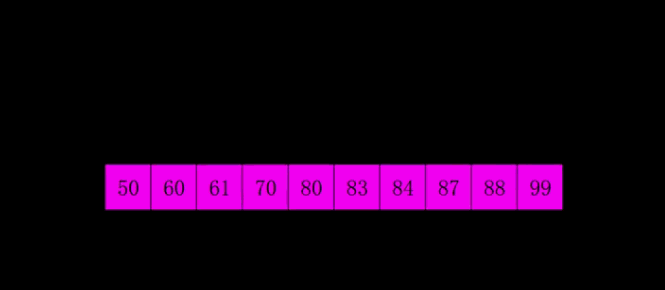
An image

javascript
function shellSort(array) {
    const length = array.length;
    //间隔
    let gap = (length / 2) | 0;
    while (gap >= 1) {
    	//以gap作为间隔分组，然后插入排序;
    	for (let i = gap; i < length; i++) {
            let temp = array[i];
            let j = i;
            while (j > gap - 1 && array[j - gap] > temp) {
            	array[j] = array[j - gap];
            	j -= gap;
            }
            array[j] = temp;
    	}
    	gap = Math.floor(gap / 2);
    }
    return array
}

6. 快速排序 ​

An image

快速排序也许是最常用的排序算法了。它的复杂度为 O(nlog(n))，且性能通常比其他复杂度 为 O(nlog(n))的排序算法要好。和归并排序一样，快速排序也使用分而治之的方法，将原始数组 分为较小的数组（但它没有像归并排序那样将它们分割开）。

  • (1) 首先，从数组中选择一个值作为主元（pivot），也就是数组中间的那个值。
  • (2) 创建两个指针（引用），左边一个指向数组第一个值，右边一个指向数组最后一个值。移 动左指针直到我们找到一个比主元大的值，接着，移动右指针直到找到一个比主元小的值，然后 交换它们，重复这个过程，直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元 之前，而比主元大的值都排在主元之后。这一步叫作划分（partition）操作。
  • (3) 接着，算法对划分后的小数组（较主元小的值组成的子数组，以及较主元大的值组成的 子数组）重复之前的两个步骤，直至数组已完全排序。
javascript
function sort(arr){
  return quick(arr, 0, arr.length - 1)
}
function quickSort(array, start, end) {
	if (start >= end) return array;
	const target = array[start];
	let l = start;
	let r = end;
	while (l < r) {
		while (l < r && array[r] >= target) {
			r--;
		}
		array[l] = array[r];
		while (l < r && array[l] < target) {
			l++;
		}
		array[r] = array[l];
	}
	array[l] = target;
	quickSort(array, start, l - 1);
	quickSort(array, l + 1, end);
	return array;
}
javascript
// 递归版本
function quick1(arr, left = 0, right = arr.length - 1) {
	if (left >= right) return;
	var i = left, j = right, flag = i;
	while(i < j) {
		while(arr[j] >= arr[flag] && j > flag) j--;
		if (i >= j) break;
		while(arr[i] <= arr[flag] && i < j) i++;
		var temp = arr[flag];
		arr[flag] = arr[j];
		arr[j] = arr[i];
		arr[i] = temp;
		flag = i
	}
	quick1(arr, left, flag - 1);
	quick1(arr, flag + 1, right);
}
// 非递归
function quick(arr, left = 0, right = arr.length - 1) {
	var list = [[left, right]]; // 模拟栈
	while(list.length > 0) {
		var now = list.pop()
		if (now[0] >= now[1]) continue;
		var i = now[0], j = now[1], flag = i;
		while(i < j) {
			while(arr[j] >= arr[flag] && j > flag) j--;
			if (i >= j) break;
			while(arr[i] <= arr[flag] && i < j)  j++;
			var temp = arr[flag];
			arr[flag] = arr[j];
			arr[j] = arr[i];
			arr[i] = temp;
			flag = i	
		}
		list.push([now[0], flag - 1]);
		list.push([flag + 1, now[1]]);
	}
}

function quickSort(array) {
	return quick(array, 0, array.length - 1)
}

function quick(array, left, right) {
	let index
	if (array.length > 1) {
		index = partition(array, left, right)
		if (left < index - 1) {
			quick(array, left, index - 1)
		}
		if (index < right) {
			quick(array, index, right)
		}
	}
	return array
}

function partition(array, left, right) {
	const pivot = array[Math.floor((right + left) / 2)]
	
	let i = left
	let j = right
	while (i <= j) {
		while (array[i] < pivot) {
			i++
		}
		
		while (array[j] > pivot) {
			j--
		}
		
		if (i <= j) {
            [array[i], array[j]] = [array[j], array[i]]
			i++
			j--
		}
	}
	return i
}

// [3,12,43,7,34,56,36] i = 0; j = 6; pivot = 7
// [3,12,43,7,34,56,36] i = 1; j = 3; pivot = 7
// [7,12,43,3,34,56,36] i = 2; j = 2; pivot = 7

7. 堆排序 ​

创建一个大顶堆，大顶堆的堆顶一定是最大的元素。

交换第一个元素和最后一个元素，让剩余的元素继续调整为大顶堆。

从后往前以此和第一个元素交换并重新构建，排序完成。

javascript
function heapSort(array) {
      creatHeap(array);
      console.log(array);
      // 交换第一个和最后一个元素，然后重新调整大顶堆
      for (let i = array.length - 1; i > 0; i--) {
        [array[i], array[0]] = [array[0], array[i]];
        adjust(array, 0, i);
      }
      return array;
    }
    // 构建大顶堆，从第一个非叶子节点开始，进行下沉操作
    function creatHeap(array) {
      const len = array.length;
      const start = parseInt(len / 2) - 1;
      for (let i = start; i >= 0; i--) {
        adjust(array, i, len);
      }
    }
    // 将第target个元素进行下沉，孩子节点有比他大的就下沉
    function adjust(array, target, len) {
      for (let i = 2 * target + 1; i < len; i = 2 * i + 1) {
        // 找到孩子节点中最大的
        if (i + 1 < len && array[i + 1] > array[i]) {
          i = i + 1;
        }
        // 下沉
        if (array[i] > array[target]) {
          [array[i], array[target]] = [array[target], array[i]]
          target = i;
        } else {
          break;
        }
      }
    }

8. 二分查找 ​

这个算法要求是被搜索的数据结构是已排序的 过程是：

  1. 选择数组的中间值
  2. 如果选中值是待搜索值，那么直接返回，算法执行完毕
  3. 如果待搜索值比选中值要小，则返回步骤一并在选中值左边的子数组中寻找（较小）
  4. 如果待搜索值比选中值要大，则返回步骤一并在选中值右边的子数组中寻找（较大）
javascript
function binarySearch(arr, target){
	let low = 0
	let high = arr.length - 1
	while (low <= high) {
		const mid = Math.floor((low + high)/2)
		const midValue = arr[mid]
		if (midValue > target) {
			high = mid - 1
		} else if (midValue < target) {
			low = mid + 1
		} else {
			return mid
		}
	}
	return -1
}

In case I don't see you. Good afternoon, good evening, and good night.

Copyright © 2019-present Notend